Black Holes

Definition of Fock space

Fock space is the (Hilbert) direct sum of tensor products of copies of a single-particle Hilbert space $H$

$F_\nu(H)=\bigoplus_{n=0}^{\infty}S_\nu H^{\otimes n} =\mathbb{C} \oplus H \oplus \left(S_\nu \left(H \otimes H\right)\right) \oplus \left(S_\nu \left( H \otimes H \otimes H\right)\right) \oplus \ldots$

Here $\mathbb{C}$ , a complex scalar, represents the states of no particles, $H$ the state of one particle, $S_\nu (H\otimes H)$ the states of two identical particles etc.

A typical state in $F_\nu(H)$ is given by

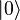$|\Psi\rangle_\nu= |\Psi_0\rangle_\nu \oplus |\Psi_1\rangle_\nu \oplus |\Psi_2\rangle_\nu \oplus \ldots = a_0 |0\rangle \oplus |\psi_1\rangle \oplus \sum_{ij} a_{ij}|\psi_{2i}, \psi_{2j} \rangle_\nu \oplus \ldots$

where

$|0\rangle$ is a vector of length 1, called the vacuum state and $\,a_0 \in \mathbb{C}$ is a complex coefficient,

$|\psi_1\rangle \in H$ is a state in the single particle Hilbert space,

$|\psi_{2i} \psi_{2j} \rangle_\nu = |\psi_{2i}\rangle|\psi_{2j}\rangle = \frac{1}{2}(|\psi_{2i}\rangle \otimes|\psi_{2j}\rangle + (-1)^\nu|\psi_{2j}\rangle\otimes|\psi_{2i}\rangle) \in S_\nu(H \otimes H)$ , and $a_{ij} = \nu a_{ji} \in \mathbb{C}$ is a complex coefficient

etc.

The convergence of this infinite sum is important if $F_\nu(H)$ is to be a Hilbert space. Technically we require $F_\nu(H)$ to be the Hilbert space completion of the algebraic direct sum. It consists of all infinite tuples $|\Psi\rangle_\nu = (|\Psi_0\rangle_\nu , |\Psi_1\rangle_\nu , |\Psi_2\rangle_\nu, \ldots)$ such that the norm, defined by the inner product is finite

$\| |\Psi\rangle_\nu \|_\nu^2 = \sum_{n=1}^\infty \langle \Psi_n |\Psi_n \rangle_\nu < \infty$

where the $n$ particle norm is defined by

$\langle \Psi_n | \Psi_n \rangle_\nu = \lim_{M\to \infty}\sum_{i_1,\ldots i_n, j_1, \ldots j_n < M}a_{i_1,\ldots, i_n}^*a_{j_1, \ldots, j_n} \langle \psi_{i_1}| \psi_{j_1} \rangle\cdots \langle \psi_{i_n}| \psi_{j_n} \rangle$

i.e. the restriction of the norm on the tensor product $H^{\otimes n}$

For two states

$|\Phi\rangle_\nu=|\Phi_0\rangle_\nu \oplus |\Phi_1\rangle_\nu \oplus |\Phi_2\rangle_\nu \oplus \ldots = b_0 |0\rangle \oplus |\phi_1\rangle \oplus \sum_{ij} b_{ij}|\phi_{2i}, \phi_{2j} \rangle_\nu \oplus \ldots$

the inner product on $F_\nu(H)$ is then defined as

$\langle \Psi |\Phi\rangle_\nu:= \sum_n \langle \Psi_n| \Phi_n \rangle_\nu = a_0^* b_0 + \langle\psi_1 | \phi_1 \rangle +\sum_{ijkl}a_{ij}^*b_{kl}\langle \phi_{2i}|\psi_{2k}\rangle\langle\psi_{2j}| \phi_{2l} \rangle_\nu + \ldots$

where we use the inner products on each of the $n$ -particle Hilbert spaces. Note that, in particular the $n$ particle subspaces are orthogonal for different $n$ .

Black Holes

Friday, 21 June 2013

Definition of Fock space

No comments:

Post a Comment

Blog Archive