Example of Fock space
An example of a pure state of the Fock space is
which describes a collection of  particles, one of which has quantum state
particles, one of which has quantum state  , another
, another  and so on up to the
and so on up to the  th particle, where each
th particle, where each  is any state from the single particle Hilbert space
is any state from the single particle Hilbert space  . Here juxtaposition is symmetric respectively antisymmetric multiplication in the symmetric and antisymmetric tensor algebra. The general state in a Fock space is a linear combination of pure states. A Fock state that cannot be written as a pure state is called an entangled state.
. Here juxtaposition is symmetric respectively antisymmetric multiplication in the symmetric and antisymmetric tensor algebra. The general state in a Fock space is a linear combination of pure states. A Fock state that cannot be written as a pure state is called an entangled state.
 particles, one of which has quantum state
particles, one of which has quantum state  , another
, another  and so on up to the
and so on up to the  th particle, where each
th particle, where each  is any state from the single particle Hilbert space
is any state from the single particle Hilbert space  . Here juxtaposition is symmetric respectively antisymmetric multiplication in the symmetric and antisymmetric tensor algebra. The general state in a Fock space is a linear combination of pure states. A Fock state that cannot be written as a pure state is called an entangled state.
. Here juxtaposition is symmetric respectively antisymmetric multiplication in the symmetric and antisymmetric tensor algebra. The general state in a Fock space is a linear combination of pure states. A Fock state that cannot be written as a pure state is called an entangled state.
When we speak of one particle in state  , it must be borne in mind that in quantum mechanics identical particles are indistinguishable. In the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are implicitly properly symmetrized. For instance, if the above state
, it must be borne in mind that in quantum mechanics identical particles are indistinguishable. In the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are implicitly properly symmetrized. For instance, if the above state  is fermionic, it will be 0 if two (or more) of the
is fermionic, it will be 0 if two (or more) of the  are equal because the anti symmetric (exterior) product
are equal because the anti symmetric (exterior) product  . This is a mathematical formulation of the Pauli exclusion principle that no two (or more) fermions can be in the same quantum state. Also, the product of orthonormal states is properly orthonormal by construction (although possibly 0 in the Fermi case when two states are equal).
. This is a mathematical formulation of the Pauli exclusion principle that no two (or more) fermions can be in the same quantum state. Also, the product of orthonormal states is properly orthonormal by construction (although possibly 0 in the Fermi case when two states are equal).
 , it must be borne in mind that in quantum mechanics identical particles are indistinguishable. In the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are implicitly properly symmetrized. For instance, if the above state
, it must be borne in mind that in quantum mechanics identical particles are indistinguishable. In the same Fock space all particles are identical (to describe many species of particles, take the tensor product of as many different Fock spaces as there are species of particles under consideration). It is one of the most powerful features of this formalism that states are implicitly properly symmetrized. For instance, if the above state  is fermionic, it will be 0 if two (or more) of the
is fermionic, it will be 0 if two (or more) of the  are equal because the anti symmetric (exterior) product
are equal because the anti symmetric (exterior) product  . This is a mathematical formulation of the Pauli exclusion principle that no two (or more) fermions can be in the same quantum state. Also, the product of orthonormal states is properly orthonormal by construction (although possibly 0 in the Fermi case when two states are equal).
. This is a mathematical formulation of the Pauli exclusion principle that no two (or more) fermions can be in the same quantum state. Also, the product of orthonormal states is properly orthonormal by construction (although possibly 0 in the Fermi case when two states are equal).
A useful and convenient basis for a Fock space is the occupancy number basis. Given the choice of a basis  of
of  , we can denote the state with
, we can denote the state with 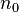 particles in state
particles in state  ,
, 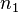 particles in state
particles in state 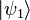 , ...,
, ...,  particles in state
particles in state  by
by
 of
of  , we can denote the state with
, we can denote the state with 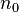 particles in state
particles in state  ,
, 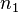 particles in state
particles in state 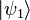 , ...,
, ...,  particles in state
particles in state  by
by
where each 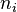 takes the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles. Such a state is called a Fock state. When the
takes the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles. Such a state is called a Fock state. When the  are understood as the steady states of a free field, the Fock states describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
are understood as the steady states of a free field, the Fock states describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
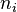 takes the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles. Such a state is called a Fock state. When the
takes the value 0 or 1 for fermionic particles and 0, 1, 2, ... for bosonic particles. Such a state is called a Fock state. When the  are understood as the steady states of a free field, the Fock states describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
are understood as the steady states of a free field, the Fock states describes an assembly of non-interacting particles in definite numbers. The most general pure state is the linear superposition of Fock states.
Two operators of great importance are the creation and annihilation operators, which upon acting on a Fock state add respectively remove a particle in the ascribed quantum state. They are denoted  and
and  respectively, with the quantum state
respectively, with the quantum state  the particle which is "added" by multiplication with
the particle which is "added" by multiplication with  respectively "removed" by (even or odd) interior product with
respectively "removed" by (even or odd) interior product with 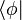 which is the adjoint of
which is the adjoint of  . It is often convenient to work with states of the basis of
. It is often convenient to work with states of the basis of  so that these operators remove and add exactly one particle in the given basis state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state
so that these operators remove and add exactly one particle in the given basis state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state  is
is  .
.
 and
and  respectively, with the quantum state
respectively, with the quantum state  the particle which is "added" by multiplication with
the particle which is "added" by multiplication with  respectively "removed" by (even or odd) interior product with
respectively "removed" by (even or odd) interior product with 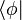 which is the adjoint of
which is the adjoint of  . It is often convenient to work with states of the basis of
. It is often convenient to work with states of the basis of  so that these operators remove and add exactly one particle in the given basis state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state
so that these operators remove and add exactly one particle in the given basis state. These operators also serve as a basis for more general operators acting on the Fock space, for instance the number operator giving the number of particles in a specific state  is
is  .
.

No comments:
Post a Comment