Motion along the line of sight in Relativistic Doppler effect
Assume the observer and the source are moving away from each other with a relative velocity  (
( is negative if the observer and the source are moving toward each other). Considering the problem in the reference frame of the source, suppose one wavefront arrives at the observer. The next wavefront is then at a distance
is negative if the observer and the source are moving toward each other). Considering the problem in the reference frame of the source, suppose one wavefront arrives at the observer. The next wavefront is then at a distance  away from him (where
away from him (where 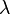 is the wavelength,
is the wavelength,  is the frequency of the wave the source emitted, and
is the frequency of the wave the source emitted, and  is the speed of light). Since the wavefront moves with velocity
is the speed of light). Since the wavefront moves with velocity  and the observer escapes with velocity
and the observer escapes with velocity  , the time (as measured in the reference frame of the source) between crest arrivals at the observer is
, the time (as measured in the reference frame of the source) between crest arrivals at the observer is
 (
( is negative if the observer and the source are moving toward each other). Considering the problem in the reference frame of the source, suppose one wavefront arrives at the observer. The next wavefront is then at a distance
is negative if the observer and the source are moving toward each other). Considering the problem in the reference frame of the source, suppose one wavefront arrives at the observer. The next wavefront is then at a distance  away from him (where
away from him (where 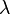 is the wavelength,
is the wavelength,  is the frequency of the wave the source emitted, and
is the frequency of the wave the source emitted, and  is the speed of light). Since the wavefront moves with velocity
is the speed of light). Since the wavefront moves with velocity  and the observer escapes with velocity
and the observer escapes with velocity  , the time (as measured in the reference frame of the source) between crest arrivals at the observer is
, the time (as measured in the reference frame of the source) between crest arrivals at the observer is
where  is the velocity of the observer in terms of the speed of light (see beta (velocity)).
is the velocity of the observer in terms of the speed of light (see beta (velocity)).
 is the velocity of the observer in terms of the speed of light (see beta (velocity)).
is the velocity of the observer in terms of the speed of light (see beta (velocity)).
Due to the relativistic time dilation, the observer will measure this time to be
where
is the Lorentz factor. The corresponding observed frequency is
The ratio
is called the Doppler factor of the source relative to the observer. (This terminology is particularly prevalent in the subject of astrophysics: see relativistic beaming.) The corresponding wavelengths are related by
and the resulting redshift
can be written as
In the non-relativistic limit (when 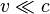 ) this redshift can be approximated by
) this redshift can be approximated by
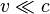 ) this redshift can be approximated by
) this redshift can be approximated by
corresponding to the classical Doppler effect.









No comments:
Post a Comment