Black Holes

Holomorphic Fock space

Holomorphic Fock space is defined to be the vector space $\mathcal F$ of holomorphic functions f(z) on C with

$\displaystyle{{1\over \pi} \iint_{\Bbb C} |f(z)|^2 e^{-|z|^2} \, dxdy}$

finite.

It has inner product

$\displaystyle{(f_1,f_2)= {1\over \pi} \iint_{\Bbb C} f_1(z)\overline{f_2(z)} e^{-|z|^2} \, dxdy.}$

$\mathcal F$ is a Hilbert space with orthonormal basis

$\displaystyle{e_n(z)={z^n\over \sqrt{n!}}}$

for n ≥ 0. Moreover the power series expansion of a holomorphic function in $\mathcal F$ gives its expansion with respect to this basis.

Thus for z in C

$\displaystyle{ |f(z)| =\left|\sum_{n\ge 0} a_n z^n\right|\le \sqrt{\pi} \|f\| e^{|z|^2/2},}$

so that evaluation at z is gives a continuous linear functional on $\mathcal F$ .

In fact

$\displaystyle{ f(a) =(f,E_a)}$

where

$\displaystyle{E_a(z)=\sum_{n\ge 0} {(E_a,e_n)z^n\over \sqrt{n!}}=\sum_{n\ge 0} {z^n\overline{a}^n\over n!} = e^{z\overline{a}}.}$

Thus in particular $\mathcal F$ is a reproducing kernel Hilbert space.

For f in $\mathcal F$ and z in C define

$\displaystyle{ W_{\mathcal F}(z)f(w)=e^{-|z|^2} e^{w\overline{z}} f(w-z).}$

Then

$\displaystyle{W_{\mathcal F}(z_1)W_{\mathcal F}(z_2)= e^{-i\Im z_1\overline{z_2}} W_{\mathcal F}(z_1+z_2),}$

so this gives a unitary representation of the Weyl commutation relations. Now

$\displaystyle{W_{\mathcal F}(a)E_0=e^{-|a|^2} E_a.}$

It follows that the representation $W_{\mathcal F}$ is irreducible.

Indeed any function orthogonal to all the E_a must vanish, so that their linear span is dense in $\mathcal F$ .

If P is an orthogonal projection commuting with W(z), let f = P E₀. Then

$\displaystyle{f(z)=(PE_0,E_z)=e^{|z|^2}(PE_0,W_{\mathcal F}(z)E_0)=(PE_{-z},E_0)=\overline{f(-z)}.}$

The only holomorphic function satisfying this condition is the constant function. So

$\displaystyle{PE_0=\lambda E_0},$

with λ = 0 or 1. Since E₀ is cyclic, it follows that P = 0 or I.

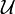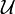By the Stone-von Neumann theorem there is a unitary operator $\mathcal U$ from L²(R) onto $\mathcal F$ , unique up to multiplication by a scalar, intertwining the two representations of the Weyl commutation relations. By Schur's lemma and the Gelfand-Naimark construction, the marix coefficient of any vector determines the vector up to a scalar multiple. 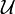Since the matrix coefficients of F = E₀ and f = H₀ are equal, it follows that the unitary $\mathcal U$ is uniquely determined by the properties

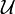$\displaystyle{W_{\mathcal F}(a) \mathcal{U} = \mathcal{U} W(a)}$

and

$\displaystyle{\mathcal{U}H_0 = E_0.}$

Hence for f in L²(R)

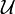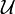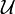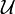$\displaystyle{\mathcal{U}f(z)= (\mathcal{U}f,E_z) = (f,\mathcal{U}^* E_z) = e^{-|z|^2}(f, \mathcal{U}^* W_{\mathcal F}(z)E_0) =e^{-|z|^2}(W(-z)f,H_0),}$

so that

$\displaystyle{\mathcal{U}f(z) ={1\over \sqrt{2\pi}}\int_{-\infty}^\infty e^{-(x^2 +y^2)} e^{-2ixy}f(t+x) e^{-t^2/2} \, dt ={1\over \sqrt{2\pi}}\int_{-\infty}^\infty B(z,t) f(t)\, dt,}$