Systematic derivation for inertial observers of Relativistic Doppler effect
Let us repeat the derivation more systematically in order to show how the Lorentz equations can be used explicitly to derive a relativistic Doppler shift equation for waves that themselves are not relativistic.
Let there be two inertial frames of reference,  and
and  , constructed so that the axes of
, constructed so that the axes of  and
and  coincide at
coincide at  , where
, where  is the time as measured in
is the time as measured in  and
and  is the time as measured in
is the time as measured in  . Let
. Let  be in motion relative to
be in motion relative to  with constant velocity
with constant velocity  ; without loss of generality, we will take this motion to be directed only along the x-axis. Thus, the Lorentz transformation equations take the form
; without loss of generality, we will take this motion to be directed only along the x-axis. Thus, the Lorentz transformation equations take the form
 and
and  , constructed so that the axes of
, constructed so that the axes of  and
and  coincide at
coincide at  , where
, where  is the time as measured in
is the time as measured in  and
and  is the time as measured in
is the time as measured in  . Let
. Let  be in motion relative to
be in motion relative to  with constant velocity
with constant velocity  ; without loss of generality, we will take this motion to be directed only along the x-axis. Thus, the Lorentz transformation equations take the form
; without loss of generality, we will take this motion to be directed only along the x-axis. Thus, the Lorentz transformation equations take the form
where  and
and  , and
, and  is the speed of light in a vacuum.
is the speed of light in a vacuum.
 and
and  , and
, and  is the speed of light in a vacuum.
is the speed of light in a vacuum.
The derivation begins with what the observer in  trivially sees. We imagine a signal source is positioned stationary at the origin,
trivially sees. We imagine a signal source is positioned stationary at the origin,  , of the
, of the  system. We will take this signal source to produce its first pulse at time
system. We will take this signal source to produce its first pulse at time  (this isevent 1) and its second pulse at time
(this isevent 1) and its second pulse at time  (this is event 2), where
(this is event 2), where  is the frequency of the signal source as the observer in
is the frequency of the signal source as the observer in  sees it. We then simply use the Lorentz transformation equations to see when and where the observer in
sees it. We then simply use the Lorentz transformation equations to see when and where the observer in  sees these two events as occurring:
sees these two events as occurring:
 trivially sees. We imagine a signal source is positioned stationary at the origin,
trivially sees. We imagine a signal source is positioned stationary at the origin,  , of the
, of the  system. We will take this signal source to produce its first pulse at time
system. We will take this signal source to produce its first pulse at time  (this isevent 1) and its second pulse at time
(this isevent 1) and its second pulse at time  (this is event 2), where
(this is event 2), where  is the frequency of the signal source as the observer in
is the frequency of the signal source as the observer in  sees it. We then simply use the Lorentz transformation equations to see when and where the observer in
sees it. We then simply use the Lorentz transformation equations to see when and where the observer in  sees these two events as occurring:
sees these two events as occurring:Observer in  | Observer in  | |||||
|---|---|---|---|---|---|---|
| Event 1 |
|
| ||||
| Event 2 |
|
|
The period between the pulses as measured by the  observer is not, however,
observer is not, however,  because event 2 occurs at a different point in space to event 1 as observed by the
because event 2 occurs at a different point in space to event 1 as observed by the  observer (that is,
observer (that is, 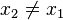 ) — we must factor in the time taken for the pulse to travel from
) — we must factor in the time taken for the pulse to travel from 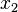 to
to  . Note that this complication is not relativistic in nature: this is the ultimate cause of the Doppler effect and is also present in the classical treatment. This transit time is equal to the difference
. Note that this complication is not relativistic in nature: this is the ultimate cause of the Doppler effect and is also present in the classical treatment. This transit time is equal to the difference  divided by the speed of the pulse as the
divided by the speed of the pulse as the  observer sees it. If the pulse moves at speed
observer sees it. If the pulse moves at speed  in
in  (negative because it moves in the negative x-direction, towards the
(negative because it moves in the negative x-direction, towards the  observer at
observer at  ), then the speed of the pulse moving towards the observer at
), then the speed of the pulse moving towards the observer at  , as
, as  sees it, is:
sees it, is:
 observer is not, however,
observer is not, however,  because event 2 occurs at a different point in space to event 1 as observed by the
because event 2 occurs at a different point in space to event 1 as observed by the  observer (that is,
observer (that is, 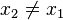 ) — we must factor in the time taken for the pulse to travel from
) — we must factor in the time taken for the pulse to travel from 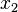 to
to  . Note that this complication is not relativistic in nature: this is the ultimate cause of the Doppler effect and is also present in the classical treatment. This transit time is equal to the difference
. Note that this complication is not relativistic in nature: this is the ultimate cause of the Doppler effect and is also present in the classical treatment. This transit time is equal to the difference  divided by the speed of the pulse as the
divided by the speed of the pulse as the  observer sees it. If the pulse moves at speed
observer sees it. If the pulse moves at speed  in
in  (negative because it moves in the negative x-direction, towards the
(negative because it moves in the negative x-direction, towards the  observer at
observer at  ), then the speed of the pulse moving towards the observer at
), then the speed of the pulse moving towards the observer at  , as
, as  sees it, is:
sees it, is:
using the Lorentz equation for the velocities, above. Thus, the period between the pulses that the observer in  measures is:
measures is:
 measures is:
measures is:
Replacing  with
with  and simplifying, we get the required result that gives the relativistic Doppler shift of any moving wave in terms of the stationary frequency,
and simplifying, we get the required result that gives the relativistic Doppler shift of any moving wave in terms of the stationary frequency,  :
:
 with
with  and simplifying, we get the required result that gives the relativistic Doppler shift of any moving wave in terms of the stationary frequency,
and simplifying, we get the required result that gives the relativistic Doppler shift of any moving wave in terms of the stationary frequency,  :
:
Ignoring the relativistic effects by taking 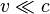 or
or  (equivalent to
(equivalent to  ) gives the classical Doppler formula:
) gives the classical Doppler formula:
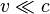 or
or  (equivalent to
(equivalent to  ) gives the classical Doppler formula:
) gives the classical Doppler formula:
For electromagnetic radiation where  the formula becomes
the formula becomes
 the formula becomes
the formula becomes
or in terms of wavelength:
where  is the wavelength of the source at the origin
is the wavelength of the source at the origin  as the observer in
as the observer in  sees it.
sees it.
 is the wavelength of the source at the origin
is the wavelength of the source at the origin  as the observer in
as the observer in  sees it.
sees it.
For electromagnetic radiation, the limit to classical mechanics,  , is instructive. The Doppler effect formula simply becomes
, is instructive. The Doppler effect formula simply becomes  . This is the correct result for classical mechanics, although it is clearly in disagreement with experiment. It is correct since classical mechanics regards the maximum speed of interaction — for electrodynamics, the speed of light — to be infinite. The Doppler effect, classical or relativistic, occurs because the wave source has time to move by the time that previous waves encounter the observer. This means that the subsequent waves are emitted further away (or closer) to the observer than they otherwise would be if the source were not in motion. The effect of this is to stretch (or compress) the wavelength of the wave as the observer encounters them. If however the waves travel instantaneously, the fact that the source is further away (or closer) makes no difference because the waves arrive at the observer no later or earlier than they would anyway since they arrive instantaneously. Thus, classical mechanics predicts that there should be no Doppler effect for light waves, whereas the relativistic theory gives the correct answer, as confirmed by experiment.
. This is the correct result for classical mechanics, although it is clearly in disagreement with experiment. It is correct since classical mechanics regards the maximum speed of interaction — for electrodynamics, the speed of light — to be infinite. The Doppler effect, classical or relativistic, occurs because the wave source has time to move by the time that previous waves encounter the observer. This means that the subsequent waves are emitted further away (or closer) to the observer than they otherwise would be if the source were not in motion. The effect of this is to stretch (or compress) the wavelength of the wave as the observer encounters them. If however the waves travel instantaneously, the fact that the source is further away (or closer) makes no difference because the waves arrive at the observer no later or earlier than they would anyway since they arrive instantaneously. Thus, classical mechanics predicts that there should be no Doppler effect for light waves, whereas the relativistic theory gives the correct answer, as confirmed by experiment.
 , is instructive. The Doppler effect formula simply becomes
, is instructive. The Doppler effect formula simply becomes  . This is the correct result for classical mechanics, although it is clearly in disagreement with experiment. It is correct since classical mechanics regards the maximum speed of interaction — for electrodynamics, the speed of light — to be infinite. The Doppler effect, classical or relativistic, occurs because the wave source has time to move by the time that previous waves encounter the observer. This means that the subsequent waves are emitted further away (or closer) to the observer than they otherwise would be if the source were not in motion. The effect of this is to stretch (or compress) the wavelength of the wave as the observer encounters them. If however the waves travel instantaneously, the fact that the source is further away (or closer) makes no difference because the waves arrive at the observer no later or earlier than they would anyway since they arrive instantaneously. Thus, classical mechanics predicts that there should be no Doppler effect for light waves, whereas the relativistic theory gives the correct answer, as confirmed by experiment.
. This is the correct result for classical mechanics, although it is clearly in disagreement with experiment. It is correct since classical mechanics regards the maximum speed of interaction — for electrodynamics, the speed of light — to be infinite. The Doppler effect, classical or relativistic, occurs because the wave source has time to move by the time that previous waves encounter the observer. This means that the subsequent waves are emitted further away (or closer) to the observer than they otherwise would be if the source were not in motion. The effect of this is to stretch (or compress) the wavelength of the wave as the observer encounters them. If however the waves travel instantaneously, the fact that the source is further away (or closer) makes no difference because the waves arrive at the observer no later or earlier than they would anyway since they arrive instantaneously. Thus, classical mechanics predicts that there should be no Doppler effect for light waves, whereas the relativistic theory gives the correct answer, as confirmed by experiment.
























No comments:
Post a Comment