The laws of black hole mechanics
The four laws of black hole mechanics are physical properties that black holes are believed to satisfy. The laws, analogous to the laws of thermodynamics, were discovered by Brandon Carter, Stephen Hawking and James Bardeen.
Statement of the laws
The laws of black hole mechanics are expressed in geometrized units.
The Zeroth Law
The horizon has constant surface gravity for a stationary black hole.
The First Law
Change of mass is related to change of area, angular momentum, and electric charge by:
where  is the mass,
is the mass,  is the surface gravity,
is the surface gravity,  is the horizon area,
is the horizon area,  is the angular velocity,
is the angular velocity,  is the angular momentum,
is the angular momentum, 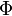 is the electrostatic potential and
is the electrostatic potential and 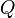 is the electric charge.
is the electric charge.
 is the mass,
is the mass,  is the surface gravity,
is the surface gravity,  is the horizon area,
is the horizon area,  is the angular velocity,
is the angular velocity,  is the angular momentum,
is the angular momentum, 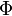 is the electrostatic potential and
is the electrostatic potential and 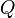 is the electric charge.
is the electric charge.The Second Law
The horizon area is, assuming the weak energy condition, a non-decreasing function of time,
This "law" was superseded by Hawking's discovery that black holes radiate, which causes both the black hole's mass and the area of its horizon to decrease over time.
The Third Law
It is not possible to form a black hole with vanishing surface gravity.  = 0 is not possible to achieve.
= 0 is not possible to achieve.
 = 0 is not possible to achieve.
= 0 is not possible to achieve.
Discussion of the laws
The Zeroth Law
The zeroth law is analogous to the zeroth law of thermodynamics which states that the temperature is constant throughout a body in thermal equilibrium. It suggests that the surface gravity is analogous to temperature. T constant for thermal equilibrium for a normal system is analogous to  constant over the horizon of a stationary black hole.
constant over the horizon of a stationary black hole.
 constant over the horizon of a stationary black hole.
constant over the horizon of a stationary black hole.The First Law
The left hand side, dM, is the change in mass/energy. Although the first term does not have an immediately obvious physical interpretation, the second and third terms on the right hand side represent changes in energy due to rotation and electromagnetism. Analogously, the first law of thermodynamics is a statement of energy conservation, which contains on its right hand side the term T dS.
The Second Law
The second law is the statement of Hawking's area theorem. Analogously, the second law of thermodynamics states that the change in entropy in an isolated system will be greater than or equal to 0 for a spontaneous process, suggesting a link between entropy and the area of a black hole horizon. However, this version violates the second law of thermodynamics by matter losing (its) entropy as it falls in, giving a decrease in entropy. Generalized second law introduced as total entropy = black hole entropy + outside entropy.
The Third Law
Extremal black holes have vanishing surface gravity. Stating that  cannot go to zero is analogous to the third law of thermodynamics which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.
cannot go to zero is analogous to the third law of thermodynamics which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.
 cannot go to zero is analogous to the third law of thermodynamics which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.
cannot go to zero is analogous to the third law of thermodynamics which states, the entropy of a system at absolute zero is a well-defined constant. This is because a system at zero temperature exists in its ground state. Furthermore, ΔS will reach zero at 0 kelvins, but S itself will also reach zero, at least for perfect crystalline substances. No experimentally verified violations of the laws of thermodynamics are known.Interpretation of the laws
The four laws of black hole mechanics suggest that one should identify the surface gravity of a black hole with temperature and the area of the event horizon with entropy, at least up to some multiplicative constants. If one only considers black holes classically, then they have zero temperature and, by the no hair theorem, zero entropy, and the laws of black hole mechanics remain an analogy. However, when quantum mechanical effects are taken into account, one finds that black holes emit thermal radiation (Hawking radiation) at temperature
From the first law of black hole mechanics, this determines the multiplicative constant of the Bekenstein-Hawking entropy which is
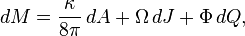
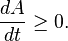


No comments:
Post a Comment