Sunday, 9 June 2013

Redshift formulae[ In a table ]

                          In general relativity one can derive several important special-case formulae for redshift in certain special spacetime geometries, as summarized in the following table. In all cases the magnitude of the shift (the value of z) is independent of the wavelength.
Redshift Summary
Redshift typeGeometryFormula
Relativistic DopplerMinkowski space (flat spacetime)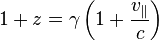1 + z = \gamma \left(1 + \frac{v_{\parallel}}{c}\right)
z \approx \frac{v_{\parallel}}{c} for small v
1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}} for motion completely in the radial direction.
1 + z=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} for motion completely in the transverse direction.
Cosmological redshiftFLRW spacetime (expanding Big Bang universe)1 + z = \frac{a_{\mathrm{now}}}{a_{\mathrm{then}}}
Gravitational redshiftany stationary spacetime (e.g. the Schwarzschild geometry)1 + z = \sqrt{\frac{g_{tt}(\text{receiver})}{g_{tt}(\text{source})}}
(for the Schwarzschild geometry, 1 + z = \sqrt{\frac{1 - \frac{2GM}{ c^2 r_{\text{receiver}}}}{1 - \frac{2GM}{ c^2 r_{\text{source} }}}}
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)