Mathematical derivation
The observational consequences of this effect can be derived using the equations from general relativity that describe a homogeneous and isotropic universe.
To derive the redshift effect, use the geodesic equation for a light wave, which is
where
 is the spacetime interval
is the spacetime interval is the time interval
is the time interval is the spatial interval
is the spatial interval is the speed of light
is the speed of light is the time-dependent cosmic scale factor
is the time-dependent cosmic scale factor is the curvature per unit area.
is the curvature per unit area.
For an observer observing the crest of a light wave at a position 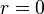 and time
and time  , the crest of the light wave was emitted at a time
, the crest of the light wave was emitted at a time  in the past and a distant position
in the past and a distant position  . Integrating over the path in both space and time that the light wave travels yields:
. Integrating over the path in both space and time that the light wave travels yields:
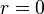 and time
and time  , the crest of the light wave was emitted at a time
, the crest of the light wave was emitted at a time  in the past and a distant position
in the past and a distant position  . Integrating over the path in both space and time that the light wave travels yields:
. Integrating over the path in both space and time that the light wave travels yields:
In general, the wavelength of light is not the same for the two positions and times considered due to the changing properties of the metric. When the wave was emitted, it had a wavelength  . The next crest of the light wave was emitted at a time
. The next crest of the light wave was emitted at a time
 . The next crest of the light wave was emitted at a time
. The next crest of the light wave was emitted at a time
The observer sees the next crest of the observed light wave with a wavelength  to arrive at a time
to arrive at a time
 to arrive at a time
to arrive at a time
Since the subsequent crest is again emitted from  and is observed at
and is observed at 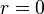 , the following equation can be written:
, the following equation can be written:
 and is observed at
and is observed at 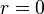 , the following equation can be written:
, the following equation can be written:
The right-hand side of the two integral equations above are identical which means
or, alternatively,
For very small variations in time (over the period of one cycle of a light wave) the scale factor is essentially a constant ( today and
today and  previously). This yields
previously). This yields
 today and
today and  previously). This yields
previously). This yields
which can be rewritten as
Using the definition of redshift provided above, the equation
is obtained. In an expanding universe such as the one we inhabit, the scale factor is monotonically increasing as time passes, thus, z is positive and distant galaxies appear redshifted.
Using a model of the expansion of the universe, redshift can be related to the age of an observed object, the so-called cosmic time–redshift relation. Denote a density ratio as Ω0:
with ρcrit the critical density demarcating a universe that eventually crunches from one that simply expands. This density is about three hydrogen atoms per thousand liters of space. At large redshifts one finds:
where H0 is the present-day Hubble constant, and z is the redshift












No comments:
Post a Comment