Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that the phase-space distribution function is constant along the trajectories of the system — that is that the density of system points in the vicinity of a given system point travelling through phase-space is constant with time.
There are also related mathematical results in symplectic topology and ergodic theory.
Liouville equations
These Liouville equations describe the time evolution of the phase space distribution function. Although the equation is usually referred to as the "Liouville equation", this equation was in fact first published by Gibbs in 1902. It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838. Consider a Hamiltonian dynamical system with canonical coordinates 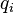 and conjugate momenta
and conjugate momenta 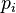 , where
, where  . Then the phase space distribution
. Then the phase space distribution  determines the probability
determines the probability  that the system will be found in the infinitesimal phase space volume
that the system will be found in the infinitesimal phase space volume  . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of  in time
in time  :
:
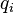 and conjugate momenta
and conjugate momenta 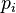 , where
, where  . Then the phase space distribution
. Then the phase space distribution  determines the probability
determines the probability  that the system will be found in the infinitesimal phase space volume
that the system will be found in the infinitesimal phase space volume  . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of  in time
in time  :
:
Time derivatives are denoted by dots, and are evaluated according to Hamilton's equations for the system. This equation demonstrates the conservation of density in phase space (which was Gibbs's name for the theorem). Liouville's theorem states that
- The distribution function is constant along any trajectory in phase space.
A simple proof of the theorem is to observe that the evolution of  is defined by the continuity equation:
is defined by the continuity equation:
 is defined by the continuity equation:
is defined by the continuity equation:
That is, the tuplet  is a conserved current. Notice that the difference between this and Liouville's equation are the terms
is a conserved current. Notice that the difference between this and Liouville's equation are the terms
 is a conserved current. Notice that the difference between this and Liouville's equation are the terms
is a conserved current. Notice that the difference between this and Liouville's equation are the terms
where  is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density,
is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density,  , is zero follows from the equation of continuity by noting that the 'velocity field'
, is zero follows from the equation of continuity by noting that the 'velocity field'  in phase space has zero divergence (which follows from Hamilton's relations).
in phase space has zero divergence (which follows from Hamilton's relations).
 is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density,
is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density,  , is zero follows from the equation of continuity by noting that the 'velocity field'
, is zero follows from the equation of continuity by noting that the 'velocity field'  in phase space has zero divergence (which follows from Hamilton's relations).
in phase space has zero divergence (which follows from Hamilton's relations).
Another illustration is to consider the trajectory of a cloud of points through phase space. It is straightforward to show that as the cloud stretches in one coordinate – 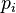 say – it shrinks in the corresponding
say – it shrinks in the corresponding 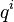 direction so that the product
direction so that the product  remains constant.
remains constant.
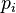 say – it shrinks in the corresponding
say – it shrinks in the corresponding 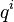 direction so that the product
direction so that the product  remains constant.
remains constant.
Equivalently, the existence of a conserved current implies, via Noether's theorem, the existence of a symmetry. The symmetry is invariant under time translations, and the generator (or Noether charge) of the symmetry is the Hamiltonian.
Physical interpretation
The expected total number of particles is the integral over phase space of the distribution:
A normalizing factor is conventionally included in the phase space measure but has here been omitted. In the simple case of an onrelativistic particle moving in Euclidean space under a force field 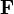 with coordinates
with coordinates  and momenta
and momenta  , Liouville's theorem can be written
, Liouville's theorem can be written
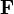 with coordinates
with coordinates  and momenta
and momenta  , Liouville's theorem can be written
, Liouville's theorem can be written
This is similar to the Vlasov equation, or the collisionless Boltzmann equation, in astrophysics. The latter, which has a 6-D phase space, is used to describe the evolution of a large number of collisionless particles moving under the influence of gravity and/or electromagnetic field.
In classical statistical mechanics, the number of particles  is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting
is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting  gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by
gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by  equal to any function of the Hamiltonian
equal to any function of the Hamiltonian  : in particular, it is satisfied by the Maxwell-Boltzmann distribution
: in particular, it is satisfied by the Maxwell-Boltzmann distribution  , where
, where  is the temperature and
is the temperature and  the Boltzmann constant.
the Boltzmann constant.
 is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting
is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting  gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by
gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by  equal to any function of the Hamiltonian
equal to any function of the Hamiltonian  : in particular, it is satisfied by the Maxwell-Boltzmann distribution
: in particular, it is satisfied by the Maxwell-Boltzmann distribution  , where
, where  is the temperature and
is the temperature and  the Boltzmann constant.
the Boltzmann constant.
See also canonical ensemble and microcanonical ensemble.





No comments:
Post a Comment