Calculations of Unruh effect
In special relativity, an observer moving with uniform proper acceleration a through Minkowski spacetime is conveniently described with Rindler coordinates. The line element in Rindler coordinates is
where  , and where
, and where 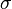 is related to the observer's proper time
is related to the observer's proper time  by
by  (here c = 1). Rindler coordinates are related to the standard (Cartesian) Minkowski coordinates by
(here c = 1). Rindler coordinates are related to the standard (Cartesian) Minkowski coordinates by
 , and where
, and where 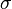 is related to the observer's proper time
is related to the observer's proper time  by
by  (here c = 1). Rindler coordinates are related to the standard (Cartesian) Minkowski coordinates by
(here c = 1). Rindler coordinates are related to the standard (Cartesian) Minkowski coordinates by
An observer moving with fixed 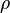 traces out a hyperbola in Minkowski space.
traces out a hyperbola in Minkowski space.
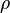 traces out a hyperbola in Minkowski space.
traces out a hyperbola in Minkowski space.
A observer moving along a path of constant 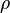 is uniformly accelerated, and is coupled to field modes which have a definite steady frequency as a function of
is uniformly accelerated, and is coupled to field modes which have a definite steady frequency as a function of 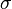 . These modes are constantly Doppler shifted relative to ordinary Minkowski time as the detector accelerates, and they change in frequency by enormous factors, even after only a short proper time.
. These modes are constantly Doppler shifted relative to ordinary Minkowski time as the detector accelerates, and they change in frequency by enormous factors, even after only a short proper time.
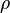 is uniformly accelerated, and is coupled to field modes which have a definite steady frequency as a function of
is uniformly accelerated, and is coupled to field modes which have a definite steady frequency as a function of 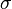 . These modes are constantly Doppler shifted relative to ordinary Minkowski time as the detector accelerates, and they change in frequency by enormous factors, even after only a short proper time.
. These modes are constantly Doppler shifted relative to ordinary Minkowski time as the detector accelerates, and they change in frequency by enormous factors, even after only a short proper time.
Translation in 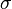 is a symmetry of Minkowski space: It is a boost around the origin. For a detector coupled to modes with a definite frequency in
is a symmetry of Minkowski space: It is a boost around the origin. For a detector coupled to modes with a definite frequency in 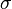 , the boost operator is then the Hamiltonian. In the Euclidean field theory, these boosts analytically continue to rotations, and the rotations close after
, the boost operator is then the Hamiltonian. In the Euclidean field theory, these boosts analytically continue to rotations, and the rotations close after 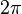 . So
. So
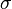 is a symmetry of Minkowski space: It is a boost around the origin. For a detector coupled to modes with a definite frequency in
is a symmetry of Minkowski space: It is a boost around the origin. For a detector coupled to modes with a definite frequency in 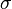 , the boost operator is then the Hamiltonian. In the Euclidean field theory, these boosts analytically continue to rotations, and the rotations close after
, the boost operator is then the Hamiltonian. In the Euclidean field theory, these boosts analytically continue to rotations, and the rotations close after 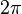 . So
. So
The path integral for this Hamiltonian is closed with period 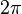 which guarantees that the H modes are thermally occupied with temperature
which guarantees that the H modes are thermally occupied with temperature  . This is not an actual temperature, because H is dimensionless. It is conjugate to the timelike polar angle
. This is not an actual temperature, because H is dimensionless. It is conjugate to the timelike polar angle 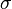 which is also dimensionless. To restore the length dimension, note that a mode of fixed frequency f in
which is also dimensionless. To restore the length dimension, note that a mode of fixed frequency f in 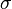 at position
at position 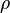 has a frequency which is determined by the square root of the metric at
has a frequency which is determined by the square root of the metric at 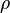 , the redshift factor. The actual inverse temperature at this point is therefore
, the redshift factor. The actual inverse temperature at this point is therefore
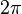 which guarantees that the H modes are thermally occupied with temperature
which guarantees that the H modes are thermally occupied with temperature  . This is not an actual temperature, because H is dimensionless. It is conjugate to the timelike polar angle
. This is not an actual temperature, because H is dimensionless. It is conjugate to the timelike polar angle 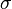 which is also dimensionless. To restore the length dimension, note that a mode of fixed frequency f in
which is also dimensionless. To restore the length dimension, note that a mode of fixed frequency f in 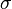 at position
at position 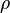 has a frequency which is determined by the square root of the metric at
has a frequency which is determined by the square root of the metric at 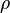 , the redshift factor. The actual inverse temperature at this point is therefore
, the redshift factor. The actual inverse temperature at this point is therefore
Since the acceleration of a trajectory at constant 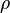 is equal to
is equal to  , the actual inverse temperature observed is
, the actual inverse temperature observed is
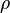 is equal to
is equal to  , the actual inverse temperature observed is
, the actual inverse temperature observed is
Restoring units yields
The Unruh effect could only be seen when the Rindler horizon is visible. If a refrigerated accelerating wall is placed between the particle and the horizon, at fixed Rindler coordinate  , the thermal boundary condition for the field theory at
, the thermal boundary condition for the field theory at  is the temperature of the wall. By making the positive
is the temperature of the wall. By making the positive 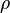 side of the wall colder, the extension of the wall's state to
side of the wall colder, the extension of the wall's state to  is also cold. In particular, there is no thermal radiation from the acceleration of the surface of the Earth, nor for a detector accelerating in a circle, because under these circumstances there is no Rindler horizon in the field of view.
is also cold. In particular, there is no thermal radiation from the acceleration of the surface of the Earth, nor for a detector accelerating in a circle, because under these circumstances there is no Rindler horizon in the field of view.
 , the thermal boundary condition for the field theory at
, the thermal boundary condition for the field theory at  is the temperature of the wall. By making the positive
is the temperature of the wall. By making the positive 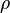 side of the wall colder, the extension of the wall's state to
side of the wall colder, the extension of the wall's state to  is also cold. In particular, there is no thermal radiation from the acceleration of the surface of the Earth, nor for a detector accelerating in a circle, because under these circumstances there is no Rindler horizon in the field of view.
is also cold. In particular, there is no thermal radiation from the acceleration of the surface of the Earth, nor for a detector accelerating in a circle, because under these circumstances there is no Rindler horizon in the field of view.
The temperature of the vacuum, seen by an isolated observer accelerated at the Earth's gravitational acceleration of g = 9.81 m/s², is only 4×10−20 K. For an experimental test of the Unruh effect it is planned to use accelerations up to 1026 m/s², which would give a temperature of about 400,000 K.
To put this in perspective, at a vacuum Unruh temperature of 3.978×10−20 K, an electron would have a de Broglie Wavelength of h/√(3mekT) = 540.85 meters, and a proton at that temperature would have a wavelength of 12.62 meters. If electrons and protons were in intimate contact in a very cold vacuum, they would have rather long wavelengths and interaction distances.
At one astronomical unit from the sun, the acceleration is GM s/AU² = 0.005932 m/s². This gives an Unruh temperature of 2.41×10−23kelvin. At that temperature, the electron and proton wavelengths are 21.994 kilometers 513 meters, respectively. Even a uranium atom will have a wavelength of 2.2 meters at such a low temperature.







No comments:
Post a Comment