Applications of Chaos theory

                     Chaos theory is applied in many scientific disciplines, including: geology, mathematics,microbiology, biology, computer science, economics,  engineering, finance,  algorithmic trading,  meteorology, philosophy, physics, politics,population dynamics,  psychology, and robotics.

Chaotic behavior has been observed in the laboratory in a variety of systems, including electrical circuits,  lasers, oscillating chemical reactions, fluid dynamics, and mechanical and magneto-mechanical devices, as well as computer models of chaotic processes. Observations of chaotic behavior in nature include changes in weather, the dynamics of satellites in the solar system, the time evolution of the magnetic field of celestial bodies, population growth in ecology, the dynamics of the action potentials in neurons, and molecular vibrations. There is some controversy over the existence of chaotic dynamics in plate tectonics  and in economics. 

Chaos theory is currently being applied to medical studies of epilepsy, specifically to the prediction of seemingly random seizures by observing initial conditions. 

Quantum chaos theory studies how the correspondence between quantum mechanics and classical mechanics works in the context of chaotic systems.  Relativistic chaos describes chaotic systems under general relativity. 

The motion of a system of three or more stars interacting gravitationally (the gravitational N-body problem) is generically chaotic. 

In electrical engineering, chaotic systems are used in communications, random number generators, and encryption systems.

In numerical analysis, the Newton-Raphson method of approximating the roots of a function can lead to chaotic iterations if the function has no real roots. 

History of Chaos theory

                                   An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits which are nonperiodic, and yet not forever increasing nor approaching a fixed point. In 1898 Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature. In the system studied, "Hadamard's billiards", Hadamard was able to show that all trajectories are unstable in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

Much of the earlier theory was developed almost entirely by mathematicians, under the name of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by G.D. Birkhoff, A. N. Kolmogorov, M.L. Cartwright and J.E. Littlewood, and Stephen Smale. Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood. Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident for some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behaviour of certain experiments like that of the logistic map. What had been beforehand excluded as measure imprecision and simple "noise" was considered by chaos theories as a full component of the studied systems.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems.

An early pioneer of the theory was Edward Lorenz whose interest in chaos came about accidentally through his work on weather prediction in 1961. Lorenz was using a simple digital computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again and to save time he started the simulation in the middle of its course. He was able to do this by entering a printout of the data corresponding to conditions in the middle of his simulation which he had calculated last time.

To his surprise the weather that the machine began to predict was completely different from the weather calculated before. Lorenz tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 was printed as 0.506. This difference is tiny and the consensus at the time would have been that it should have had practically no effect. However Lorenz had discovered that small changes in initial conditions produced large changes in the long-term outcome. Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modelling cannot in general make long-term weather predictions. Weather is usually predictable only about a week ahead.

In 1963, Benoît Mandelbrot found recurring patterns at every scale in data on cotton prices. Beforehand, he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy. Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards). This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device. Arguing that a ball of twine appears to be a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (for example, the Menger sponge, the Sierpiński gasket and the Koch curve or "snowflake", which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1975 Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory. Biological systems such as the branching of the circulatory and bronchial systems proved to fit a fractal model.

Chaos was observed by a number of experimenters before it was recognized; e.g., in 1927 by van der Pol and in 1958 by R.L. Ives. However, as a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on Nov. 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.

In December 1977 the New York Academy of Sciences organized the first symposium on Chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw (a physicist, part of the Eudaemons group with J. Doyne Farmer and Norman Packard who tried to find a mathematical method to beat roulette, and then created with them the Dynamical Systems Collective in Santa Cruz, California), and the meteorologist Edward Lorenz.

The following year, Mitchell Feigenbaum published the noted article "Quantitative Universality for a Class of Nonlinear Transformations", where he described logistic maps. Feigenbaum notably discovered the universality in chaos, permitting an application of chaos theory to many different phenomena.

In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum "for his brilliant experimental demonstration of the transition to turbulence and chaos in dynamical systems".

Then in 1986 the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on Chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking disorder among schizophrenics. This led to a renewal of physiology in the 1980s through the application of chaos theory, for example in the study of pathological cardiac cycles.

In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in Physical Review Letters describing for the first time self-organized criticality (SOC), considered to be one of the mechanisms by which complexity arises in nature.

Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behaviour. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including: earthquakes (which, long before SOC was discovered, were known as a source of scale-invariant behaviour such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law  describing the frequency of aftershocks); solar flares; fluctuations in economic systems such as financial markets(references to SOC are common in econophysics); landscape formation; forest fires; landslides; epidemics; and biological evolution(where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These "applied" investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.

This same year 1987, James Gleick published Chaos: Making a New Science, which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public, (though his history under-emphasized important Soviet contributions). At first the domain of work of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in The Structure of Scientific Revolutions (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by J. Gleick.

The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory continues to be a very active area of research, involving many different disciplines (mathematics, topology, physics, population biology, biology, meteorology, astrophysics, information theory, etc.).

                          Chaos theory

                    Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, engineering, economics and biology. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the butterfly effect. Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.  This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.  In other words, the deterministic nature of these systems does not make them predictable.  This behavior is known as deterministic chaos, or simply chaos. This was summarised by Edward Lorenz as follows: 

Chaos: When the present determines the future, but the approximate present does not approximately determine the future.

Chaotic behavior can be observed in many natural systems, such as weather.  Explanation of such behavior may be sought through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps.  

Chaotic dynamics

In common usage, "chaos" means "a state of disorder".  However, in chaos theory, the term is defined more precisely. Although there is no universally accepted mathematical definition of chaos, a commonly used definition says that, for a dynamical system to be classified as chaotic, it must have the following properties: 

1. it must be sensitive to initial conditions;
2. it must be topologically mixing; and
3. its periodic orbits must be dense.

The requirement for sensitive dependence on initial conditions implies that there is a set of initial conditions of positive measure which do not converge to a cycle of any length.

Sensitivity to initial conditions

Sensitivity to initial conditions means that each point in such a system is arbitrarily closely approximated by other points with significantly different future trajectories. Thus, an arbitrarily small perturbation of the current trajectory may lead to significantly different future behaviour. However, it has been shown that the last two properties in the list above actually imply sensitivity to initial conditions   and if attention is restricted to intervals, the second property implies the other two  (an alternative, and in general weaker, definition of chaos uses only the first two properties in the above list).  It is interesting that the most practically significant condition, that of sensitivity to initial conditions, is actually redundant in the definition, being implied by two (or for intervals, one) purely topological conditions, which are therefore of greater interest to mathematicians.

Sensitivity to initial conditions is popularly known as the "butterfly effect", so called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C. entitled Predictability: Does the Flap of a Butterfly’s Wings in Brazil set off a Tornado in Texas? The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different.

A consequence of sensitivity to initial conditions is that if we start with only a finite amount of information about the system (as is usually the case in practice), then beyond a certain time the system will no longer be predictable. This is most familiar in the case of weather, which is generally predictable only about a week ahead. 

The Lyapunov exponent characterises the extent of the sensitivity to initial conditions. Quantitatively, two trajectories in phase space with initial separation  diverge

where λ is the Lyapunov exponent. The rate of separation can be different for different orientations of the initial separation vector. Thus, there is a whole spectrum of Lyapunov exponents — the number of them is equal to the number of dimensions of the phase space. It is common to just refer to the largest one, i.e. to the Maximal Lyapunov exponent (MLE), because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.

There are also measure-theoretic mathematical conditions (discussed in ergodic theory) such as mixing or being a K-system which relate to sensitivity of initial conditions and chaos.

Topological mixing

Topological mixing (or topological transitivity) means that the system will evolve over time so that any given region or open set of its phase space will eventually overlap with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points will eventually become widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behaviour: all points except 0 will tend to positive or negative infinity.

Density of periodic orbits

Density of periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits.  The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example,  →  →  (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem). 

Sharkovskii's theorem is the basis of the Li and Yorke  (1975) proof that any one-dimensional system which exhibits a regular cycle of period three will also display regular cycles of every other length as well as completely chaotic orbits.

Strange attractors

Some dynamical systems, like the one-dimensional logistic map defined by x→ 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behaviour is found only in a subset of phase space. The cases of most interest arise when the chaotic behaviour takes place on an attractor, since then a large set of initial conditions will lead to orbits that converge to this chaotic region.

An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it was not only one of the first, but it is also one of the most complex and as such gives rise to a very interesting pattern which looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors which arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set which forms at the boundary between basins of attraction of fixed points – Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and a fractal dimension can be calculated for them.

Minimum complexity of a chaotic system

Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. In contrast, for continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Finite dimensional linear systems are never chaotic; for a dynamical system to display chaotic behaviour it has to be either nonlinear, or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two dimensional differential equation has very regular behavior. The Lorenz attractor discussed above is generated by a system of three differential equations with a total of seven terms on the right hand side, five of which are linear terms and two of which are quadratic (and therefore nonlinear). Another well-known chaotic attractor is generated by the Rossler equations with seven terms on the right hand side, only one of which is (quadratic) nonlinear. Sprott  found a three dimensional system with just five terms on the right hand side, and with just one quadratic nonlinearity, which exhibits chaos for certain parameter values. Zhang and Heidel  showed that, at least for dissipative and conservative quadratic systems, three dimensional quadratic systems with only three or four terms on the right hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two dimensional surface and therefore solutions are well behaved.

While the Poincaré–Bendixson theorem means that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behaviour.  Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite-dimensional.  A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis.

    Convergence of the ergodic means in the L^p norms 

Let (X, Σ, μ) be as above a probability space with a measure preserving transformation T, and let 1 ≤ p ≤ ∞. The conditional expectation with respect to the sub-σ-algebra Σ_T of the T-invariant sets is a linear projector E_T of norm 1 of the Banach space L^p(X, Σ, μ) onto its closed subspace L^p(X, Σ_T, μ) The latter may also be characterized as the space of all T-invariant L^p-functions on X. The ergodic means, as linear operators on L^p(X, Σ, μ) also have unit operator norm; and, as a simple consequence of the Birkhoff–Khinchin theorem, converge to the projector E_T in the strong operator topology of L^p if 1 ≤ p ≤ ∞, and in the weak operator topology if p = ∞. More is true if 1 < p ≤ ∞ then the Wiener–Yoshida–Kakutani ergodic dominated convergence theorem states that the ergodic means of ƒ ∈ L^pare dominated in L^p; however, if ƒ ∈ L¹, the ergodic means may fail to be equidominated in L^p. Finally, if ƒ is assumed to be in the Zygmund class, that is |ƒ| log⁺(|ƒ|) is integrable, then the ergodic means are even dominated in L¹.

Mean ergodic theorem

               Von Neumann's mean ergodic theorem, holds in Hilbert spaces. 

Let U be a unitary operator on a Hilbert space H; more generally, an isometric linear operator (that is, a not necessarily surjective linear operator satisfying ‖Ux‖ = ‖x‖ for all x in H, or equivalently, satisfying U*U = I, but not necessarily UU* = I). Let P be the orthogonal projection onto {ψ ∈ H| Uψ = ψ} = Ker(I - U).

Then, for any x in H, we have:

where the limit is with respect to the norm on H. In other words, the sequence of averages

converges to P in the strong operator topology.

This theorem specializes to the case in which the Hilbert space H consists of L² functions on a measure space and U is an operator of the form

where T is a measure-preserving endomorphism of X, thought of in applications as representing a time-step of a discrete dynamical system. The ergodic theorem then asserts that the average behavior of a function ƒ over sufficiently large time-scales is approximated by the orthogonal component of ƒ which is time-invariant.

In another form of the mean ergodic theorem, let U_t be a strongly continuous one-parameter group of unitary operators on H. Then the operator

converges in the strong operator topology as T → ∞. In fact, this result also extends to the case of strongly continuous one-parameter semigroup of contractive operators on a reflexive space.

Remark: Some intuition for the mean ergodic theorem can be developed by considering the case where complex numbers of unit length are regarded as unitary transformations on the complex plane (by left multiplication). If we pick a single complex number of unit length (which we think of as U), it is intuitive that its powers will fill up the circle. Since the circle is symmetric around 0, it makes sense that the averages of the powers of U will converge to 0. Also, 0 is the only fixed point of U, and so the projection onto the space of fixed points must be the zero operator (which agrees with the limit just described).

Ergodic theorems

                   Let T: X → X be a measure-preserving transformation on a measure space (X, Σ, μ) and suppose ƒ is a μ-integrable function, i.e. ƒ ∈L¹(μ). Then we define the following averages:

Time Average: This is defined as the average (if it exists) over iterations of T starting from some initial point x:

Space Average: If μ(X) is finite and nonzero, we can consider the space or phase average of ƒ:

In general the time average and space average may be different. But if the transformation is ergodic, and the measure is invariant, then the time average is equal to the space average almost everywhere. This is the celebrated ergodic theorem, in an abstract form due to George David Birkhoff. (Actually, Birkhoff's paper considers not the abstract general case but only the case of dynamical systems arising from differential equations on a smooth manifold.) The equidistribution theorem is a special case of the ergodic theorem, dealing specifically with the distribution of probabilities on the unit interval. More precisely, the pointwise or strong ergodic theorem states that the limit in the definition of the time average of ƒ exists for almost every x and that the (almost everywhere defined) limit function ƒ̂ is integrable:

Furthermore, ƒ̂ is T-invariant, that is to say

holds almost everywhere, and if μ(X) is finite, then the normalization is the same:

In particular, if T is ergodic, then ƒ̂ must be a constant (almost everywhere), and so one has that

almost everywhere. Joining the first to the last claim and assuming that μ(X) is finite and nonzero, one has that

for almost all x, i.e., for all x except for a set of measure zero. For an ergodic transformation, the time average equals the space average almost surely. As an example, assume that the measure space (X, Σ, μ) models the particles of a gas as above, and let ƒ(x) denotes the velocity of the particle at position x. Then the pointwise ergodic theorems says that the average velocity of all particles at some given time is equal to the average velocity of one particle over time.

Ergodic theory

                                        Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics.

A central concern of ergodic theory is the behavior of a dynamical system when it is allowed to run for a long time. The first result in this direction is the Poincaré recurrence theorem, which claims that almost all points in any subset of the phase space eventually revisit the set. More precise information is provided by various ergodic theorems which assert that, under certain conditions, the time average of a function along the trajectories exists almost everywhere and is related to the space average. Two of the most important examples are ergodic theorems of Birkhoff and von Neumann. For the special class of ergodic systems, the time average is the same for almost all initial points: statistically speaking, the system that evolves for a long time "forgets" its initial state. Stronger properties, such as mixing and equidistribution, have also been extensively studied.

The problem of metric classification of systems is another important part of the abstract ergodic theory. An outstanding role in ergodic theory and its applications to stochastic processes is played by the various notions of entropy for dynamical systems.

The concepts of ergodicity and the ergodic hypothesis are central to applications of ergodic theory. The underlying idea is that for certain systems the time average of their properties is equal to the average over the entire space. Applications of ergodic theory to other parts of mathematics usually involve establishing ergodicity properties for systems of special kind. In geometry, methods of ergodic theory have been used to study the geodesic flow on Riemannian manifolds, starting with the results of Eberhard Hopf for Riemann surfaces of negative curvature. Markov chains form a common context for applications in probability theory. Ergodic theory has fruitful connections with harmonic analysis, Lie theory (representation theory, lattices in algebraic groups), and number theory (the theory ofdiophantine approximations, L-functions).

Ergodic transformations

Ergodic theory is often concerned with ergodic transformations. The intuition behind such transformations, which act on a given set, is that they do a thorough job "stirring" the elements of that set. (E.g., if the set is a quantity of hot oatmeal in a bowl, and if a spoon of syrup is dropped into the bowl, then iterations of the inverse of an ergodic transformation of the oatmeal will not allow the syrup to remain in a local subregion of the oatmeal, but will distribute the syrup evenly throughout. At the same time, these iterations will not compress or dilate any portion of the oatmeal: they preserve the measure that is density.) Here is the formal definition.

Let T: X → X be a measure-preserving transformation on a measure space (X, Σ, μ), with μ(X) = 1. A measure-preserving transformation T as above is ergodic if for every E in Σ with T⁻¹(E) = E either μ(E) = 0 or μ(E) = 1.

Liouville's theorem (Hamiltonian)

In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that the phase-space distribution function is constant along the trajectories of the system — that is that the density of system points in the vicinity of a given system point travelling through phase-space is constant with time.

There are also related mathematical results in symplectic topology and ergodic theory.

Liouville equations

These Liouville equations describe the time evolution of the phase space distribution function. Although the equation is usually referred to as the "Liouville equation", this equation was in fact first published by Gibbs in 1902.  It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838.  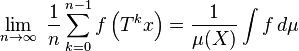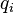Consider a Hamiltonian dynamical system with canonical coordinates  and conjugate momenta 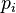, where . Then the phase space distribution  determines the probability  that the system will be found in the infinitesimal phase space volume . The Liouville equation governs the evolution of  in time :

Time derivatives are denoted by dots, and are evaluated according to Hamilton's equations for the system. This equation demonstrates the conservation of density in phase space (which was Gibbs's name for the theorem). Liouville's theorem states that

The distribution function is constant along any trajectory in phase space.

A simple proof of the theorem is to observe that the evolution of  is defined by the continuity equation:

That is, the tuplet  is a conserved current. Notice that the difference between this and Liouville's equation are the terms

where  is the Hamiltonian, and Hamilton's equations have been used. That is, viewing the motion through phase space as a 'fluid flow' of system points, the theorem that the convective derivative of the density, , is zero follows from the equation of continuity by noting that the 'velocity field'  in phase space has zero divergence (which follows from Hamilton's relations).

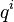Another illustration is to consider the trajectory of a cloud of points through phase space. It is straightforward to show that as the cloud stretches in one coordinate –  say – it shrinks in the corresponding  direction so that the product  remains constant.

Equivalently, the existence of a conserved current implies, via Noether's theorem, the existence of a symmetry. The symmetry is invariant under time translations, and the generator (or Noether charge) of the symmetry is the Hamiltonian.

Physical interpretation

The expected total number of particles is the integral over phase space of the distribution:

A normalizing factor is conventionally included in the phase space measure but has here been omitted. In the simple case of an onrelativistic particle moving in Euclidean space under a force field  with coordinates  and momenta , Liouville's theorem can be written

This is similar to the Vlasov equation, or the collisionless Boltzmann equation, in astrophysics. The latter, which has a 6-D phase space, is used to describe the evolution of a large number of collisionless particles moving under the influence of gravity and/or electromagnetic field.

In classical statistical mechanics, the number of particles  is very large, (typically of order Avogadro's number, for a laboratory-scale system). Setting  gives an equation for the stationary states of the system and can be used to find the density of microstates accessible in a given statistical ensemble. The stationary states equation is satisfied by  equal to any function of the Hamiltonian : in particular, it is satisfied by the Maxwell-Boltzmann distribution , where  is the temperature and  the Boltzmann constant.

See also canonical ensemble and microcanonical ensemble.

Examples of Phase space

        Low dimensions

                     For simple systems, there may be as few as one or two degrees of freedom. One degree of freedom occurs when one has an autonomous ordinary differential equation in a single variable,  with the resulting one-dimensional system being called a phase line, and the qualitative behaviour of the system being immediately visible from the phase line. The simplest non-trivial examples are the exponential growth model/decay (one unstable/stable equilibrium) and the logistic growth model (two equilibria, one stable, one unstable).

The phase space of a two-dimensional system is called a phase plane, which occurs in classical mechanics for a single particle moving in one dimension, and where the two variables are position and velocity. In this case, a sketch of the phase portrait may give qualitative information about the dynamics of the system, such as the limit cycle of the Van der Pol oscillator shown in the diagram.

Here, the horizontal axis gives the position and vertical axis the velocity. As the system evolves, its state follows one of the lines (trajectories) on the phase diagram.

Chaos theory

Classic examples of phase diagrams from chaos theory are :

• the Lorenz attractor
• population growth (i.e. Logistic map)
• parameter plane of complex quadratic polynomials with Mandelbrot set.

Phase space

                               In mathematics and physics, a phase space is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables (i.e. the cotangent space of configuration space). The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. 

A plot of position and momentum variables as a function of time is sometimes called a phase plot or a phase diagram. Phase diagram, however, is more usually reserved in the physical sciences for a diagram showing the various regions of stability of the thermodynamic phases of a chemical system, which consists of pressure, temperature, and composition.

In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system, or allowed combination of values of the system's parameters, a point is plotted in the multidimensional space. Often this succession of plotted points is analogous to the system's state evolving over time. In the end, the phase diagram represents all that the system can be, and its shape can easily elucidate qualities of the system that might not be obvious otherwise. A phase space may contain a great many dimensions. For instance, a gas containing many molecules may require a separate dimension for each particle's x, y and z positions and momenta as well as any number of other properties.

In classical mechanics, any choice of generalized coordinates q ⁱ for the position (i.e. coordinates on configuration space) defines conjugate generalized momenta p_i which together define co-ordinates on phase space. More abstractly, in classical mechanics phase space is the cotangent space of configuration space, and in this interpretaton the procedure above expresses that a choice of local coordinates on configuration space induces a choice of natural local Darboux coordinates for the standard symplectic structure on a cotangent space.

The motion of an ensemble of systems in this space is studied by classical statistical mechanics. The local density of points in such systems obeys Liouville's Theorem, and so can be taken as constant. Within the context of a model system in classical mechanics, the phase space coordinates of the system at any given time are composed of all of the system's dynamical variables. Because of this, it is possible to calculate the state of the system at any given time in the future or the past, through integration of Hamilton's or Lagrange's equations of motion.